中学生の科目のなかでも数学は、特に差がついてしまいがち。そこで、今回は数学の習熟度別に分けて勉強方法をご紹介します。
目次
まずは「どの段階」でわからなくなったのかをチェック
 保護者
保護者
教室長、よく「数学は積み重ね」だなんて言うけど、なぜなんですか?
 教室長
教室長
たとえば「電気」と「植物」。これらはどちらも「理科」とひとくくりにされますが、実際に勉強する内容は大きく違いますよね。
 保護者
保護者
確かに。理科は、横に広く学んでいくイメージがあるわね。
 教室長
教室長
それに比べ数学は、算数のころから学ぶことが1本の線でつながっている単元が多いんです。京子さんの言葉をお借りするなら、知識を縦に縦に、上に上にと積んでいくイメージでしょうか。
 保護者
保護者
なるほど。だから「数学は積み重ね」なんですね。
 教室長
教室長
ええ。では積み重ねていく上で、下の段が不安定だったらどうなるでしょう?
 保護者
保護者
それ以上、上積みができない?
 教室長
教室長
その通り。かけ算が理解できなければ、割り算も理解できません。だから基礎の段階で足場が固まっていない生徒さんは、次の段階になってもついていけないケースが多いんです。
 保護者
保護者
だからこそ、自分がニガテな範囲をしっかり把握することが大切になりそうね。
 教室長
教室長
そうなんです。ちなみに中学校の数学で習う単元は、おおまかにこのようにまとめることができます。
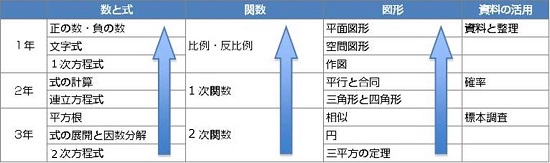
(表:数学範囲)
 保護者
保護者
それぞれグループに分けることができるんですね。
 教室長
教室長
そうなんです。「資料の活用」の中にはありませんが、ほかのものにはいずれも矢印が入っているのがわかると思います。矢印は「わからなくなったら、ひとつ上にさかのぼってみる」という意味です。たとえば中学2年の「1次関数」が解けなかったら、中学1年の「比例・反比例」まで戻ってやり直してみる。このように、たとえそれが前の学年や小学校の算数で学ぶ範囲だったとしても、いったんわからなくなった地点まで戻り、基礎を固めなおすことが大切です。
 保護者
保護者
「戻り学習」というわけですね。でもそれって、生徒さんにとっては結構つらいことなんじゃ…。
 教室長
教室長
確かに一見遠回りのようにも見えるし、気乗りしないこともあるかもしれません。しかしここでいったん戻る勇気を持てないと、これからニガテ意識はさらに強くなってしまうことでしょう。
わからない範囲が把握できたら?反復練習で目指せ70点!
 保護者
保護者
では、自分がわからない範囲を把握できたら、実際にどうすればいいんですか?
 教室長
教室長
とにかくできるところからその範囲の問題を繰り返し解き、順を追ってステップアップしていくことです。
 保護者
保護者
なぜ反復練習が大切なんですか?
 教室長
教室長
数学で学ぶべきは「解き方のパターン」です。このパターンのストックをいくつ持っているかが、テストの得点と比例すると言っても過言ではありません。
 保護者
保護者
それは方程式を暗記するということですか?
 教室長
教室長
ただ覚えるというよりも、「この問題にはこのパターンだ!」といったように、実際に使いこなせるかがポイントです。ここで言う「パターン」は、問題を解くための道具とも言えるでしょうか。
 保護者
保護者
道具を「知っている」のと実際に「使える」のは、違うということですね。
 教室長
教室長
おっしゃる通りです。パターンの使い方を体に染み込ませるために、反復練習や復習が大切なのです。習ってきたことの基礎パターンさえモノにしていれば、数学がもともと苦手なお子さんでもテストで70点以上をとることも難しくはありません。
 保護者
保護者
反復練習とは、具体的にどんな解き方をしたらいいんでしょう?問題をたくさん解くから、問題集は数冊用意したほうがいいんですか?
 教室長
教室長
いえ、使う問題集は1冊だけです。何種類もの問題集に手を出すより、1冊の問題集を何回も繰り返し、完璧にすることが大事です。
 保護者
保護者
では同じ問題を、何回ぐらい解けばいいんですか?
 教室長
教室長
わからない問題は、最低でも3〜4回は解いておきたいところです。まず1回目は問題を解こうとせずに、いきなり解説を読んでしまうぐらいで構いません。わからない問題を無理に解こうとするのは、効率的ではありませんからね。
 保護者
保護者
本番は2回目以降なんですね。
 教室長
教室長
はい。そして2回目は、それぞれの問題にマークをつけていきます。
◯=簡単に解けた
△ =だいたい解けた
×=解けなかったが、解説を見れば理解できた
△は◯になるように、×は△になるように、何度も何度も同じ解説を読み、パターンを定着させていきます。
 保護者
保護者
◯のつかなかった問題を重点的に勉強するんですね。
 教室長
教室長
テストで8〜9割がとれるまでブラッシュアップするには?
 保護者
保護者
さらに高得点を目指すには、応用問題への対策も必要ですよね。基礎と応用では、全然問題内容が違うような気もしますけど…。
 教室長
教室長
基礎問題がパターン1つで解ける問題だとすれば、応用問題というのは、パターンを2つ3つ組み合わせて解く問題だといえます。応用問題を解くための鍵は、これまでに増やしてきた基礎パターンをいかに適切に組み合わせられるかなんです。
 保護者
保護者
なるほど。基礎があっての応用だと。
 教室長
教室長
そうです。まずは「戻り学習」をして、わからないところを確実になくす。それから応用問題を繰り返し解いてみる。そうすることで、複数のパターンの使い方に慣れることができます。
 保護者
保護者
やはりここでも積み重ねが大事なんですね。あと教室長、うちの子は計算ミスが減らないようで、本当に困っています。どうしたらいいのかしら。
 教室長
教室長
計算ミスが多い生徒さんは、途中式をしっかりと書かない傾向にあります。お子さんはいかがですか?
 保護者
保護者
言われてみれば「答えが出ればいいんでしょ!」なんて言って、式はあんまりちゃんと書いていないかも!
 教室長
教室長
途中式を丁寧に書いていれば、後から見直した時に、どこで間違えたのか気付くこともできます。こういった習慣が、計算ミスを減らしてくれますよ。
 保護者
保護者
なるほど、ポンと答えだけ書いているようではダメなのね。
 教室長
教室長
そして計算ミスをした問題にはチェックをつけておき、もう一度後から解きなおしてみましょう。これも計算ミスをなくすためには大切なことです。
 保護者
保護者
やはり反復練習が欠かせないんですね。
 教室長
教室長
ええ。数学は積み重ねですから。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。
















