【中１数学】「文字式」って何？　どうやって式をたてるの？

文字式ってどうやって表すの？

文字式って何だろう？

文字式とは、以下のような式のことです。

数字だけでなく、a，x，y などの文字も使って表していますね。左の2つの式が表す意味はなんとなくわかりそうです。
10+a　・・・　10とaを足す
x－5　 ・・・　xから5を引く

ですが、3xや というのは、どういう式なのでしょうか。
これを理解するには、文字式のきまりを知らなくてはなりません。

 

文字式の表し方のきまり

 

「文字式のきまり？また覚えることが増えるのか・・・。」
といった声が聞こえてきそうですが、覚えておくべき基本ルールは以下の２つだけなので、それほど難しいものではありません。

 

①かけ算は“×”を省き、わり算は分数の形で書きましょう！
●例

 

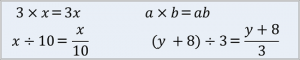
②同じ文字をかけたものは、～乗の形にしましょう！
●例

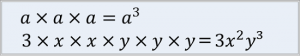
和や差については数字のみの式と同じで、10+a や x－5 のように、“＋” や “－”の記号でつなげるだけです。では、練習問題を通してみていきましょう。

 

個別指導塾の基本問題に挑戦！

■問題
次の式を、文字式の表し方にしたがって表しなさい。

（１）　c×(-5)×b
（２）　4×x+(-1)×y
（３） （x－5）÷（－3）

 

□答え
（１）　-5bc 
文字は数字の前に書き、文字はふつうアルファベット順に書きます。

（２）　4x-y
文字の前の１は省略して書きます。

（３）

分母の“マイナス”は分数の前に書きます。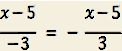

かけ算は“×”を省き、わり算は分数の形で書きます。

 

なぜ文字を使うの？

次に、「どうして式の中に文字を入れるの？？」という疑問に答えていきましょう。それは、「文字を使うことで全ての数について表すことができる」からです。そういわれてもピンときませんね。では、具体的な例でみてみましょう。

 

１つの式で表すために文字を使う！

 

例えば、次のような課題を考えます。
50円の箱に、1個180円のケーキを何個か入れて買ったとき、ケーキと箱の代金の合計を文字式で表してみましょう。
この代金の合計の求め方をまずは言葉で表してみると、

（ケーキ1個の値段） × （ケーキの個数）+（箱代）

ですね。ここに、問題文から読み取って、あてはまる数を入れていくと、ケーキ1個の代金は180円、箱代は50円となります。さて、ケーキの個数については具体的な数が書いてありません。何個買ったかわからないので、ひとまずケーキを□個買うことにしましょう。すると、代金は、

180 × □ + 50　（円）

という式で表せます。この□にはいろいろな数を入れることができます。つまり、この１つの式で「ケーキを何個か買ったときの代金」を表せるのです。
ですが□のような記号だと、具体的な数がわからないものが複数あったときに困ってしまいますよね…。そこで、文字の登場です！つまり、「変わる数やわからない数がある場合、それを文字を使って表す」のです。どのような文字でもいいのですが、ここではxを使いましょう。すると、

＊ケーキを１個買う場合
　・・・180 × １+ 50（円）

＊ケーキを２個買う場合
　・・・180 × ２+ 50（円）

＊ケーキを３個買う場合
　・・・180 × ３+ 50（円）
 
というのを、
＊ケーキをx個買う場合
　・・・180 × x + 50 ＝ 180 x ＋ 50（円）
という１つの式で表現できるのです。
したがって、１個180円のケーキをx個買って、50円の箱に入れてもらう場合の代金は、(180x＋50)円と表すことができます。

こうやって文字を使って表してしておけば、わからなかった数（これを未知数や変数などとと呼びます）、ここでは「個数」が決まったときに、次のように、xのところに数を入れる（これを代入といいます）ことでサッと計算ができて便利なのです。

ケーキを５個買う場合　     　
180 ×５+ 50 ＝ 900 ＋ 50 ＝ 950 (円) 
（xのところに５を入れます）

ケーキを12個買う場合          
180 ×12+ 50 ＝ 2160 ＋ 50 ＝ 2210 (円) 
（xのところに12を入れます）

 

文字式をたてるにはどうするの？

文字式の意味、表し方がわかったところで、次は問題文から文字式をたてられるようにしていきましょう。ここまでの説明が長かったので大変そうにみえるかもしれませんが、手順はそれほど多くはないので、安心してください。

 

文字式をたてる手順は３ステップ！

数量を文字式で表すときのポイントは、
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
①言葉を使った式で表してみる
②その言葉にあてはまる数や文字を考える
③式をつくる
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
といった３ステップで行うことです。先ほどの、ケーキの代金を思い出してみましょう。

■例
50円の箱に、1個180円のケーキをx個入れて買ったとき、ケーキと箱の代金の合計を文字式で表しなさい。

□解説
①代金の求め方を言葉で表すと、（ケーキ1個の代金） × （ケーキの個数）+（箱代）

②ケーキ1個の値段は180円、ケーキの個数はx個、箱代は50円

③したがって、代金は 180× x＋50　より、 (180x＋50)円
これだけの手順で、文字式をたてることができるのです。では、練習問題に挑戦してみましょう。

 

個別指導塾の基本問題に挑戦！

■問題１
１枚300円の入場券をx枚買うのに、3000円出したときのおつりを、文字を使った式で表しなさい。

□解説
①おつりの求め方を言葉で表すと、（出したお金）－（代金）

②出したお金は、3000円。代金は、１枚300円で、それをx枚買うから、300 × x ＝ 300 x  （円）

③したがって、おつりは(3000－300 x）円 

 

■問題２
底辺がxcm、高さが10cmの三角形の面積を、文字を使った式で表しなさい。

□解説
①三角形の面積を求める公式は、 (底辺)×(高さ)÷２

②底辺はxcm、高さは10cm

③したがって、面積は　x × 10 ÷ ２ ＝= ５x cm²

いかがでしょう？　問題文から条件を読み取って式をたてていくことは、とても大切です。１つずつ手順を踏んで考えていくことが数学の問題を解くコツなのです。

 

個別指導塾の応用問題パワーアップドリルに挑戦！

それでは最後に、実力をつけていくための応用問題に挑戦しましょう。

■応用問題
図のような正四角柱があります。【例】のように、次の式が何を表しているのか答えなさい。

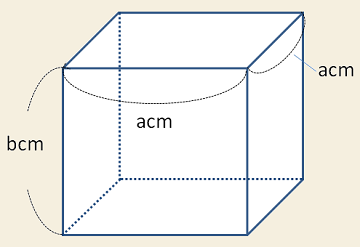
【例】 4a cm → 底面の正方形の周の長さ

(1)（2a2 ＋4ab）cm²
(2)  a 2b cm³

 

□答え 
(1) 正四角柱の表面の面積
(2) 正四角柱の体積

 

応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。今回は文字式を使った表し方について解説をしました。ケーキの代金に関する問題の中でも、

「文字式の表し方がわからない」
「代金の求め方を言葉で表すことができない」
「言葉で表した式に数や文字をあてはめることができない」

など、つまずくポイントはお子さんによってさまざまです。場合によっては算数の内容にさかのぼって復習をする必要があるかもしれません。
数学は「積み上げ学習」と言われており、以前の学年で習った内容をもとに、発展した学習を積み上げていきます。そのため、「わからない」を残さないように、仕組みや考え方などをしっかりと理解しながら進めていくことが非常に大切なのです。

もし、「お子さんのテストの点数がわるい」「勉強がうまくいっていない」「授業についていけていない」などでお悩みの方は、個別指導塾での指導方法がきっと役に立ちます。ぜひ個別指導塾の無料学習相談会などの機会を利用して、学習のプロにぜひご相談ください。