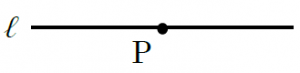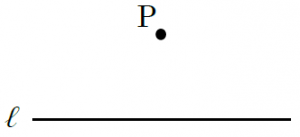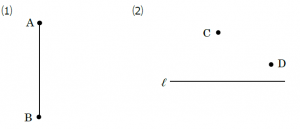数学の中では、角度に注目することがよくあります。角度として最もよく見るのは、垂直ではないでしょうか。直角三角形、正方形、長方形などの図形で扱いますね。さて、今回は、垂直な線、垂線について、作図の仕方を通して確認していきましょう。

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
指定された点を通る垂線をかいてみよう!
「直角」「垂直」「垂線」の違いって?
まずは、言葉について確認しましょう。「直角」「垂直」は、次のように表されます。
| ・90°の角のことを直角という。 ・2本の直線が交わってできる角が直角のとき、その2本の直線は垂直であるという。 |
この「直角」「垂直」という2つの言葉はよく間違えやすいのですが、「直角」は90°の角の大きさや形を表すい葉で「垂直」は2つの直線の交わり方を表す言葉です。また、垂直であることを、「⊥」という記号を使って表します。

「垂線」は、次のように表されます。
| ・2直線が垂直であるとき、一方の直線を他方の直線の垂線という。 |
上の図でいうと、「直線ℓは直線mの垂線」「直線mは直線ℓの垂線」ということです。
中学1年生では、この垂線の作図について学びます。その作図の方法をみていきましょう。
直線上にある点を通る垂線のかき方
ある点を通る垂線のかき方についてみていきます。大きく2種類あります。まずは、直線上にある点を通る垂線のかき方についてです。
|
≪例題≫
|
次の手順で行います。
① 点Pにコンパスの針をおき、直線ℓと2点で交わるように円の一部をかく。
② ①でできた交点の1つに針をおき、弧をかく。
③ ②のときと同じ半径の円の弧を、①でできたもう1つの交点に針をおいてかく。
④ ②③でかいた弧の交点と点Pを通る直線をかく。この直線が答えとなる。
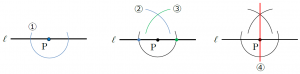
さて、ここでの重要なポイントは、「②と③のときにコンパスの開き方を変えてはいけない」ということです。
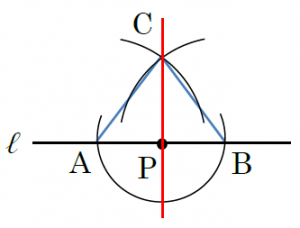
図のように交点をA、B、Cとします。①の作図からAP=BP、②と③の作図からAC=BC、CPが共通していることから、3辺の長さがそれぞれ等しいので、△APCと△BPCが合同といえます。よって、∠APC=∠BPC=90°となるので、直線CPが垂線であるといえます。
ここで、②と③でコンパスの開き方を変えてしまうと、合同ではなくなってしまうのです。①と②、③で変えるのは問題ありませんが、②と③では変えてはいけないことには注意が必要です。
直線上にない点を通る垂線のかき方
次は、直線上にない点を通る垂線のかき方をみてみましょう。
|
≪例題≫
|
次の手順で行います。実は先ほどと同じ流れでかくことができます。
① 点Pにコンパスの針をおき、直線ℓと2点で交わるように弧をかく。
② ①でできた交点の1つに針をおき、弧をかく。(①とコンパスの開き方は変えてもよい。)
③ ②のときとコンパスの開き方を変えずに、①でできたもう1つの交点に針をおいて、②の線と交わるように弧をかく。
④ ②③でかいた弧の交点と点Pを通る直線をかく。この直線が答えとなる。
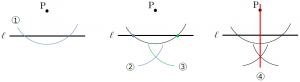
こちらも、②と③でコンパスの開き方を変えてはいけないことが注意点です。ここで紹介した2つの垂線のかき方は、作図の基本となります。確実に身につけておくことが必要です。
個別指導塾の基本問題に挑戦!
|
≪例題≫
|
≪答え≫
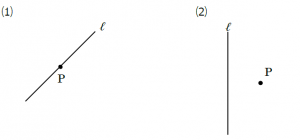
向きが変わっても作図の手順は同じです。例題と同じように作図します。
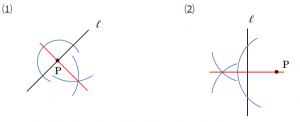
効率的・効果的な学習法なら個別指導塾へお任せ
垂直二等分線をかいてみよう!
垂直二等分線ってどんな線?
「垂直二等分線」は次のように表されます。
| ・ある線分の中点を通り、その線分に垂直な直線を垂直二等分線という。 |
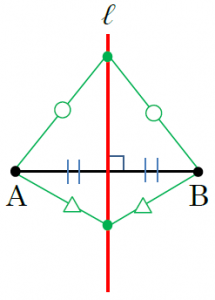
下の図において、直線ℓは線分ABの垂直二等分線です。この垂直二等分線は、とても重要な性質を持っています。それは、「直線ℓ上のすべての点は、2点A、Bからの距離が等しい」ということです。この、「2点から距離が等しい点の集まり」という性質を利用した作図の問題がたくさん出てきます。垂直二等分線の作図のしかただけでなく、この性質も覚えておくことが重要なポイントとなります。
垂直二等分線を作図してみよう!
では、垂直二等分線の作図のしかたをみていきましょう。
|
≪例題≫
|
次の手順で行います。
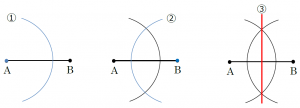
① 点Aにコンパスの針をおき、弧をかく。
② ②のときとコンパスの開き方を変えずに、点Bにコンパスの針をおき、②の線と2点で交わるように弧をかく。
③ ①と②でかいた弧の2つの交点を結んだ直線が答えとなる。
重要なポイントは、「①と②のときにコンパスの開き方を変えてはいけない」ということです。その理由は、先ほど紹介した「直線ℓ上のすべての点は、2点A、Bからの距離が等しい」という性質を利用しているからです。①と②でコンパスの開き方を変えてしまうと、①と②でかいた弧の交点と2点A、Bのそれぞれとの距離が異なってしまうからです。このポイントをしっかりとおさえておくことが大切です。
個別指導塾の基本問題に挑戦!
|
≪問題≫
|
≪答え≫
⑴ 向きが変わっても作図の手順は同じです。例題と同じように作図します。
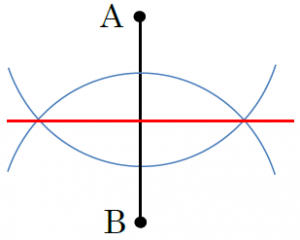
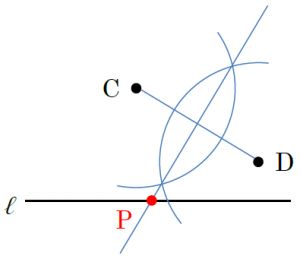
⑵は、「2点C、Dから距離が等しい」とありますから、まず、2点C、Dを結び、線分CDの垂直二等分線をひきます。この線と直線ℓの交点がPとなります。このとき、必ず「P」と図の中にかくことを忘れないようにしましょう。
個別指導塾の応用問題に挑戦!
|
≪応用問題≫
|
≪答え≫
≪解説≫
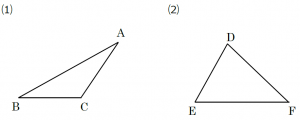
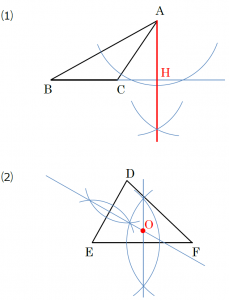
⑴ 点Aを通り、直線BCに垂直な直線をかく。ただし、線分BCでは線が足りないので、はじめにCの方向に直線をのばす。
⑵ 3点D、E、Fを通る円の中心がOということは、OD、OE、OFの長さが等しいということである。すなわち、3点D、E、Fからの距離が等しい点を作図すればよい。線分DE、線分EF、線分FDのそれぞれの垂直二等分線のうち2つをかいて、その交点がOとなる。
応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。今回は垂線について解説しました。この内容では、
・垂線や垂直二等分線の作図のしかたがわからない。
・向きが変わってしまうと何をしていいのかわからなくなる。
・問題文から何を作図してよいのかわからない。
など、つまずくポイントはお子さんによってさまざまです。
数学は「積み上げ学習」といわれており、以前の学年で習った内容や算数の内容をもとに、発展した学習を積み上げていきます。特に、今回学んだ、垂線の作図のしかたや垂直二等分線の性質などは、先の単元にも出てきます。できるだけ「わからない」を残さないように、きちんと身につけておくことが大切です。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。