【中１数学】イメージがわきにくい図形の対称移動を徹底解説！

対称移動とは直線を折り目として折り返す移動！

対称移動とはどんな移動？

図形の対称移動とはどんな移動か覚えていらっしゃいますでしょうか？　教科書などでは次のように表されます。

具体的に図で見てみましょう。

例えば、下の図において△ＡＢＣを直線ℓを折り目として折り返すと△Ａ′Ｂ′Ｃ′のようになります。つまり、△Ａ′Ｂ′Ｃ′は△ＡＢＣを対称移動させた図形ということになります。

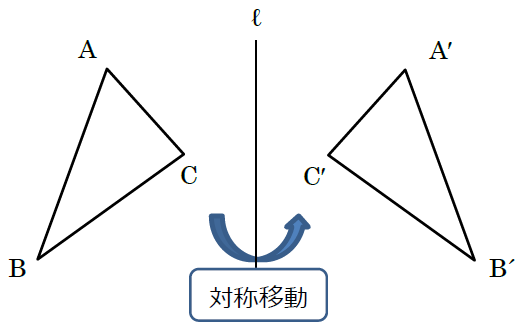
ここで、それぞれの頂点の移動に注目してみましょう。点Ａは点Ａ′、点Ｂは点Ｂ′、点Ｃは点Ｃ′に移動しています。このとき、それぞれを対応する頂点といいます。また、△Ａ′Ｂ′Ｃ′は△ＡＢＣを直線ℓで折り返してできていますから、２つの対応する頂点と直線ℓとの距離はそれぞれ等しくなります。このことから、この２つの対応する頂点を結んでみると、次の図のような関係があることがわかります。

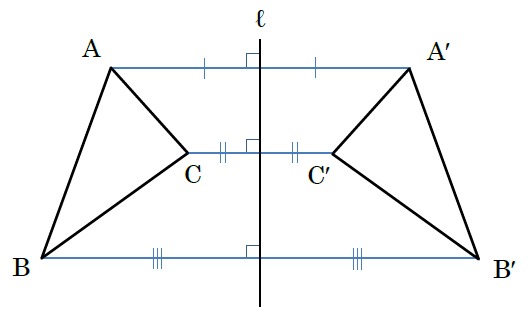
つまり、直線ℓは２つの対応する頂点を結んだ線分の垂直二等分線になっているのです。この性質に関する問題はよくテストなどで出題されます。どのような問題か見てみましょう。

《例題》
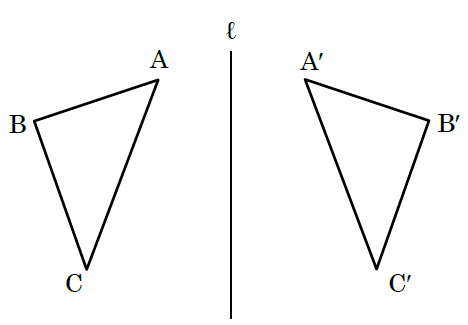
次の図のように、直線ℓを対称の軸として△ＡＢＣを対称移動させて△Ａ′Ｂ′Ｃ′をかいた。次の問いに答えなさい。
⑴　線分ＡＡ′と直線ℓの関係を記号を使って表しなさい。
⑵　線分ＢＢ′と直線ℓの交点をＭとする。線分ＢＭと線分Ｂ′Ｍの長さの関係を式で表しなさい。
⑶　線分ＣＣ′と直線ℓの交点をＮとする。線分ＣＣ′と線分ＣＮの長さの関係を式で表しなさい。

直線ℓは、２つの対応する頂点を結んだ線分の垂直二等分線になっていますから、次の図のような関係になっています。

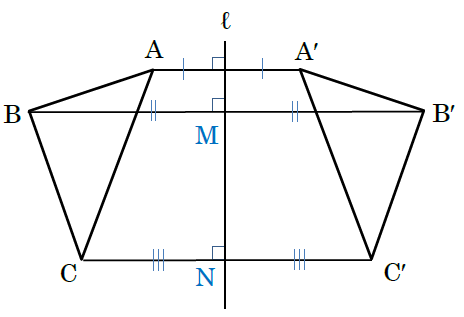
⑴は、線分ＡＡ′と直線ℓは垂直なので、答えは、ＡＡ′⊥ℓ
⑵は、点Ｍは線分ＢＢ′の中点なので、答えは、ＢＭ＝Ｂ′Ｍ
⑶は、点Ｎは線分ＣＣ′の中点なので、線分ＣＣ′の長さは線分ＣＮの２倍である。
よって、答えは、ＣＣ′＝２ＣＮ　

いかがでしょうか。問題となると少々難しそうにみえますが、「対称軸が２つの対応する頂点を結んだ線分の垂直二等分線である」ことさえわかっていれば実は難しくはないのです。特徴をきちんと押さえておけば、基本問題は解けるということを伝えてあげてください。

東京個別・関西個別（個別指導塾）の基本問題に挑戦！

では、先ほどの例題を参考にお子さんと一緒に、問題に取り組んでみてください。

《問題》
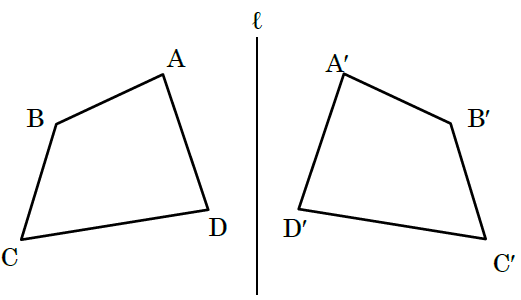
次の図のように、直線ℓを対称の軸として四角形ＡＢＣＤを対称移動させて四角形Ａ′Ｂ′Ｃ′Ｄ′をかいた。次の問いに答えなさい。
⑴ 直線ℓと垂直な線分をすべて答えなさい。
⑵　線分ＢＢ′と直線ℓとの交点をＭとする。線分ＢＭと長さが等しい線分を答えなさい。
⑶　線分ＤＤ′と直線ℓの交点をＮとする。長さが線分ＤＤ′の半分である線分をすべて答えなさい。

《答え》
直線ℓは、２つの対応する頂点を結んだ線分の垂直二等分線なので、次の図のような関係になっています。

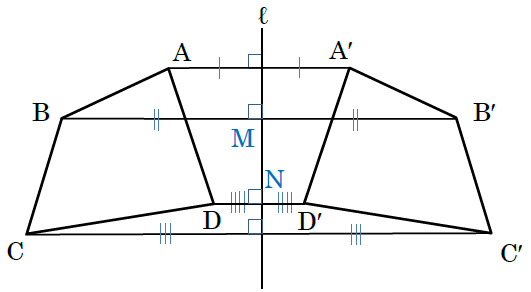
⑴　２つの対応する頂点を結んだ線分は直線ℓに垂直なので、答えは、線分ＡＡ′、線分ＢＢ′、線分ＣＣ′、線分ＤＤ′
⑵　点Ｍは線分ＢＢ′の中点なので、線分ＢＭと長さが等しいのは、線分Ｂ′Ｍ
⑶　点Ｎは線分ＤＤ′の中点なので、長さが線分ＤＤ′の半分であるのは、線分ＤＮと線分Ｄ′Ｎ

対称移動したあとの図形の位置を見つけよう！

対称の軸と対応する頂点からの距離の関係を利用！

ここでは、ある図形を対称移動したあとの図形の位置を見つけてみましょう。重要なポイントは、「２つの対応する頂点と対称の軸からの距離はそれぞれ等しい」ことを利用することです。次の例題を通して見ていきましょう。

《例題》
次の図において、△ＡＢＣを、直線ℓを対称の軸として対称移動させた△Ａ′Ｂ′Ｃ′をかきなさい。

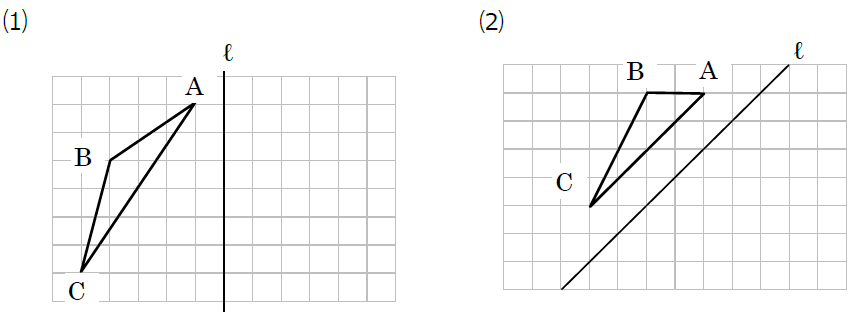
⑴は対称の軸がマス目の水平な線と垂直になっていますので、点Ａ、Ｂ、Ｃを右にまっすぐ移動させればよいですね。
点Ａから右に１マス進むと直線ℓにつきます。そこからさらに右に１マス進んだところが点Ａ′の位置です。同様に、点Ｂと直線ℓの距離は4マス、点Ｃと直線ℓの距離は5マスですので、答えは次の図のようになります。

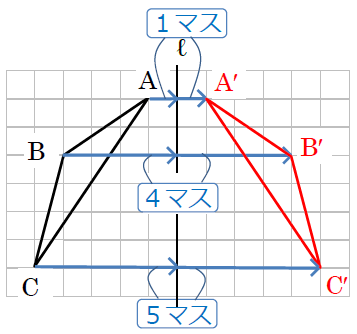
⑵は、対称の軸が右に１マス進むとき上に１マス進む直線ですので、直線ℓと垂直になるには、右に１マス進むとき下に１マス進むようにすればよいですね。
点Ａから右に1マス、下に1マス進むと直線ℓにつきます。そこからさらに右に1マス、下に1マス進んだところが点Ａ′の位置です。同様に、点Ｂから直線ℓまでは右に2マス、下に2マスで、点Ｃから直線ℓまでは右に1マス、下に1マスですから、答えは次の図のようになります。

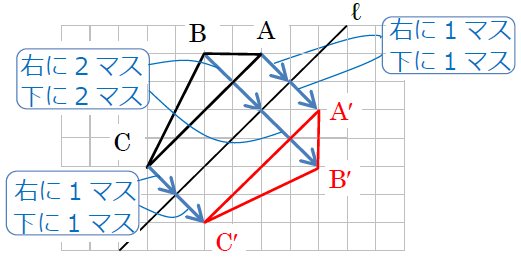
⑵のようなときにどうすればいいか困ってしまうお子さまが見られます。横と縦をそれぞれで考えるということがポイントです。

東京個別・関西個別（個別指導塾）の基本問題に挑戦！

例題と図形の形は違いますが、同じように考えれば解ける問題です。挑戦してみてください。

《問題》
次の図において、四角形ＡＢＣＤを、直線ℓを対称の軸として対称移動させた四角形Ａ′Ｂ′Ｃ′Ｄ′をかきなさい。

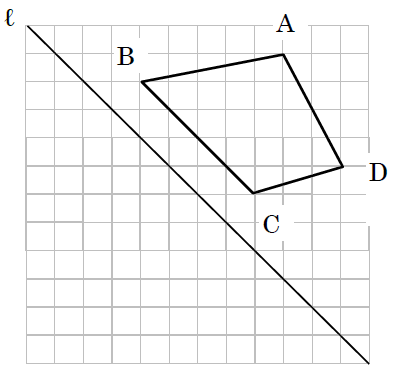
《答え》
対称の軸が右に１マス進むとき下に１マス進む直線ですから、直線ℓと垂直になるには左に1マス進むとき下に１マス進めばよいですね。点Ａから左に４マス、下に４マス進むと直線ℓにつき、そこからさらに左に４マス、下に４マス進んだところが点Ａ‘の位置になります。
同様に、点Ｂから直線ℓまでは左に１マス、下に１マス、点Ｃから直線ℓまでは左に1マス、下に1マス、点Ｄから直線ℓまでは左に３マス、下に３マスですから、答えは次の図のようになります。

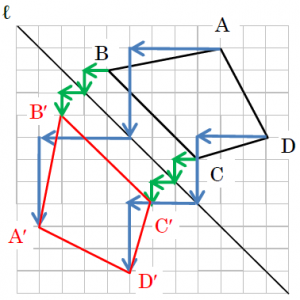
今回は、図形の対称移動について解説しました。ここで扱ったものは基礎的な問題です。応用問題では複数の移動方法を絡めた問題や、関数のグラフと絡めた問題など実に多様な問題が出題されます。そのため、どこでつまずかくかはお子さんによって異なります。これらの応用問題を解けるようになるためには１人ひとりのつまずきポイントやニガテポイントをしっかりと解消する必要があります。ただ、つまずきポイントやニガテポイントを発見するのは、少し時間がかかるかもしれません。お子さんのつまずきやニガテを早く解消したい場合は、個別指導のプロに相談してみるのもよいでしょう。