中学2年の数学では、いくつかの図形の性質について学びます。今回は、その中でもよく出てくる二等辺三角形についてみていきます。二等辺三角形の性質は中学3年生の図形の内容でも頻繁に出てきますので、確実に押さえておくことが重要です。また、なかなか区別ができずに困ってしまう「定義」と「定理」についても詳しく解説します。言葉の意味をしっかり覚えることは大切ですので、ぜひお子さんにも教えてあげてください。

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
二等辺三角形とはどういう三角形?
定義と定理は違う?
図形の性質を扱うときに出てくる用語が「定義」と「定理」です。この2つの区別ができないお子さんが多くいらっしゃいます。この2つの違いを明確にしておくことがポイントです。
二等辺三角形とは?と聞かれたとき、いろいろな回答が考えられますが、
・2つの辺の長さが等しい三角形
・2つの角の大きさが等しい三角形
・ひし形を対角線で切った一方の三角形
どれが正解でしょうか?
どれも正解です。ただし、質問に対する回答として最も適しているのは、
・2つの辺の長さが等しい三角形
です。定義とは言葉の意味をはっきりと述べたもののことです。小学校では、「2つの辺の長さが等しい三角形を二等辺三角形という」と学びました。これが二等辺三角形の定義になります。
では、そのほかの二等辺三角形の説明は、何なのか? これは、
「二等辺三角形とは、2つの辺の長さが等しい三角形」
と決めたときに、証明された事柄と考えるといいでしょう。
この、
「二等辺三角形とは、2つの辺の長さが等しい三角形」
のように、言葉の意味をはっきりと述べたものを、定義と言います。対して、
「二等辺三角形の2つの角の大きさは等しい」
「二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する」
のように、定義をもとに証明された事柄の中で大切なものを定理と言います。
つまり、「二等辺三角形とは2つの辺の長さが等しい三角形」(定義)をもとにして、「二等辺三角形の2つの角の大きさは等しい」(定理)を証明することができます。
二等辺三角形以外の三角形の定義を確認しよう!
三角形の種類をいくつ覚えていらっしゃいますか? 「定義」とともに確認しましょう。
角度によって定義された三角形
・直角三角形…1つの角が直角である三角形
・鋭角三角形…3つの角がすべて鋭角である三角形
・鈍角三角形…1つの角が鈍角である三角形
三角定規に代表される直角三角形。多くの人が、三角形というとこの形と思い浮かべるであろう鋭角三角形。つぶれたイメージの鈍角三角形。これらの三角形は、突然、問題の条件として出てくることもあります。これらの三角形の名前や特徴をきちんと覚えられるようにしておくことが大切です。
辺の関係によって定義された三角形
・二等辺三角形…2つの辺の長さが等しい三角形
・正三角形…3つの辺の長さが等しい三角形
この2つのうち、特に正三角形は特別で、すべての辺の長さが等しいのですべての角の大きさも等しく、1つの角の大きさは180°÷3=60°です。また、3つの辺の長さが等しいので、もちろん、2つの辺が等しい三角形の仲間です。つまり、正三角形は、二等辺三角形でもあります。
大切なことは、「定義をしっかり覚えたうえで、定理と区別しておくこと」です。ただし、定義と定理は混同しないように注意です。そうでないと数学的な事柄を説明する、つまり、証明するときに、根拠とするのは何か?が変わってしまいます。
二等辺三角形に関する定理を確認しよう!
いろいろな種類の三角形の定義を確認したところで、今度は「定理」について確認しましょう。
定理は定義をもとに証明された事柄の中で大切なものでしたね。二等辺三角形ならば、どういう結論を示すことができるでしょう。
ここで大事なのは、「仮定と結論の関係をきちんとつかむこと」です。
例えば、次の文章を見てみましょう。
「A君が東京都に住んでいる」 ならば 「A君は日本に住んでいる」である。
この文章の中では、「A君が東京都に住んでいる」が仮定で「A君は日本に住んでいる」が結論です。この文章は、正しいですね。しかし、仮定と結論を入れ替えてみてください。
「A君が日本に住んでいる」 ならば 「A君は東京都に住んでいる」である。
この文章は正しいでしょうか? 日本には、東京都だけでなく、大阪府、愛知県、福岡県など、さまざまな都道府県がありますね。よって、正しくありません。このように、仮定と結論の関係を入れ違えてしまうと間違いになることがあります。仮定と結論の関係をしっかりとつかむようにすることが大切です。
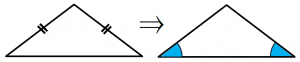
定理 二等辺三角形の底角
二等辺三角形の底角は等しい
定理 二等辺三角形の頂角の二等分線
二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する。
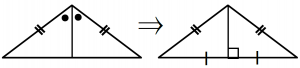
*頂角・・・長さの等しい2つの辺の間の角
*底辺・・・頂角に対する辺
*底角・・・底辺の両端の角
二等辺三角形の定義や定理はとても重要な性質ですので、正確に覚えるように伝えてください。では、これらを利用した問題についてみていきましょう。
二等辺三角形に関する基本問題を解いてみよう!
二等辺三角形の底角は等しい!
二等辺三角形の定義や定理は角度を求めるときや証明で利用されます。ここでは、角度を求める問題についてみていきます。
|
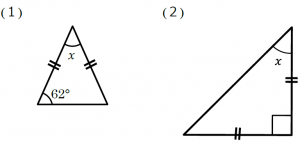
《例題》
|
二等辺三角形の定理「二等辺三角形の底角は等しい」から、ポイントは二等辺三角形の底角を見つけることです。
⑴は、1つの底角の大きさが62°なので、もう1つの底角の大きさも62°です。三角形の内角の和が180°(定理)なので、
X=180°−2×62°=56°
⑵は、頂角が直角で、底角の大きさがxです。だから、(1)と同様に考えて、
X=(180°−90°)÷2=45°
今回の問題は、二等辺三角形の角の大きさを求める問題でした。ですから、「二等辺三角形の底角は等しい」が使えないかと考えることが大切になります。二等辺三角形の定義や定理をしっかりと頭に入れておかないと、問題を見たときにどうすればよいかがわからなくなります。まずは定義や定理を区別して理解し、いろいろな問題に取り組めるようにしましょう。
二等辺三角形を作図しよう!
次は作図の問題をみてみましょう。ここでは二等辺三角形の定義「二等辺三角形の2つの辺の長さは等しい」を利用しています。
| 《例題》 底辺の長さが2㎝、等しい辺の長さが3㎝の二等辺三角形を、定規とコンパスとものさしを使って作図しなさい。 |
次の手順で底辺の長さが2㎝、等しい辺の長さが3㎝の二等辺三角形を作図します。
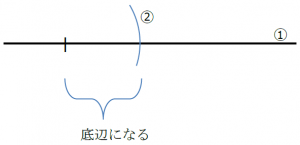
1.底辺をかく。
①定規で、長めの直線を引きます。
②かいた直線上に、1か所印をつけ、ものさしからコンパスに2㎝の長さをうつし、コンパスの針を、印をつけた直線上の点にあてて円弧をかき、2㎝の底辺の端を決めます。
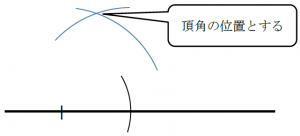
2.頂角の位置を決める。
ものさしからコンパスに3㎝の長さをうつし、コンパスの針を底辺の端にあてて円弧をかきます。両端に対してこの操作を行い、2つの円弧の交わった点を頂角の位置とします。
3.頂角と底辺の両端を、それぞれ定規を使って線分で結ぶ。
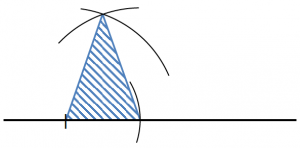
「コンパスは円をかくもの」というイメージが強いですが、コンパスの一番の利点は同じ長さを測りとれることです。二等辺三角形の定義は「2つの辺の長さが等しい三角形」ですから、コンパスを使って作図をすることができます。
効率的・効果的な学習法なら個別指導塾へお任せ
東京個別・関西個別(個別指導塾)の基本問題に挑戦!
では次の問題にお子さんと一緒に取り組んでみてください。問題文からどの三角形の定義や定理を利用すればよいかを考えることがポイントです。
| 《問題》 定規とコンパスを使って、60°の角を作図しなさい。 |
60°の角をもつ三角形を思い浮かべてみてください。そう、正三角形ですね。3つの辺の長さが等しい三角形をかくつもりになって、作図をします。
《答えの例》
1.底辺をかく。
①定規で、長めの直線を引きます。
②かいた直線上に1か所印をつけ、コンパスの針を印をつけた直線上の点にあてて円弧をかきます。
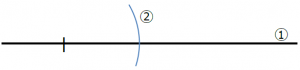
2.頂角の位置を決める。
コンパスの針を底辺の端にあてて1と同じ半径の円弧をかきます。両端に対してこの操作を行い、2つの円弧の交わった点を頂角の位置とします。
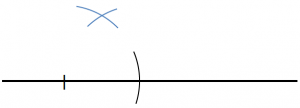
3.底辺の端と円弧の交わった点を、定規を使って直線で結ぶ。
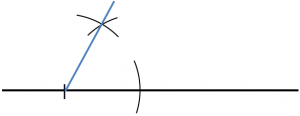
この問題では「60°」といわれたときに「正三角形」をイメージできることがポイントです。三角形の定義や定理を頭に入れておくことがやはり重要なのです。このことをしっかりと押さえるように教えてあげてください。
二等辺三角形に関する証明問題を解いてみよう!
三角形の合同条件を確認しよう!
二等辺三角形についての理解を深めるために証明問題についてみていきましょう。二等辺三角形に関する証明問題では三角形の合同が使われることがありますが、合同条件を覚えていらっしゃいますでしょうか。三角形の合同条件は、それが決まれば、作図できる条件とも言えます。作図のイメージと合わせて、3つの合同条件を確認しましょう。
1.3組の辺がそれぞれ等しい。
ここまでで確認した三角形の作図の方法と一緒です。
2.2組の辺とその間の角がそれぞれ等しい。
定規と分度器を使って角を作り、コンパスで2組の辺の長さを決めてもう1辺を定規で結んでかけば、三角形をかけます。
3.1組の辺とその両端の角がそれぞれ等しい。
定規とコンパスを使って底辺をかき、分度器で両端の角を決めて定規で結べば、三角形をかけます。
図形に関する証明問題は、合同な三角形を見つけて、対応する辺や角が等しいことを利用して証明することも多いです。図をかいて、補助線を引いたりしてみながら、証明問題に取り組むことが大切です。では、証明の問題をみてみましょう。
東京個別・関西個別(個別指導塾)の基本問題に挑戦!
| 《問題》 二等辺三角形の頂角の二等分線は、底辺を垂直に2等分することを証明しなさい。 |
《答え》
証明
AB=ACの二等辺三角形の頂角Aの二等分線と辺BCの交点をDとする。
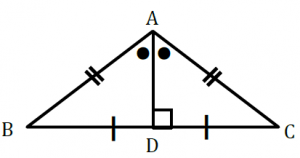
△ABDと△ACDに注目する。
△ABCがAB=ACの二等辺三角形なので、
AB=AC ……①
ADは、∠BACの二等分線なので、∠BAD=∠CAD……②
また、 辺ADは共通 ……③
①、②、③より、2組の辺とその間の角がそれぞれ等しいから
△ABD≡△ACD
合同な図形の対応する辺や角は等しいので、 BD=CD
また、∠ADB=∠ADCで、∠ADB+∠ADC=180°より、
∠ADB=90°
すなわち、 AD⊥BC
この問題文を見て気づかれたでしょうか。この問題は二等辺三角形の定理の1つ「二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する」を証明する問題なのです。また、途中では二等辺三角形の定義を使用しています。
二等辺三角形に限らず、図形の定義や定理を区別して理解することが第一歩になります。その際に、言葉だけでなく図とともに理解するということを大切にすれば理解しやすくなります。ぜひお子さんにもそのように教えてあげてください。
東京個別・関西個別(個別指導塾)の応用問題に挑戦!
では、ステップアップとして応用問題に挑戦してみてください。
|
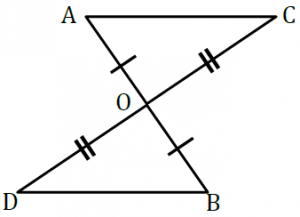
《応用問題》
|
《答え》
証明
△AOCと△BODにおいて、
仮定より、AO=BO ……①、CO=DO ……②
対頂角は等しいので、∠AOC=∠BOD ……③
①、②、③より、2組の辺とその間の角がそれぞれ等しいから
△AOC≡△BOD
よって、合同な図形の対応する角は等しいので、∠ACO=∠BDO
したがって、錯角が等しいので、AC//DB
《解説》
この問題は、基本問題よりも少しだけ難しいです。平行であることを示すためには、何を言えればよいのかを探さなければならないからです。
証明問題は、合同条件などを覚えているだけでは対応できません。「何が言えたら何を示せたことになるか?」を考えることこそ大事です。
今回は、二等辺三角形の定義と定理、三角形の合同の証明や、作図について解説しました。図形の問題では覚えるべきことが多いためにつまずいてしまうお子さまがよくみられます。また、それぞれの図形の性質に加えて、それまでに習ったことと関連付けられることが多く、
・作図の仕方が分からない
・三角形の合同条件を覚えていない
など、過去の内容を覚えていないためにつまずいてしまうお子さまも多くいます。
数学は「積み上げ学習」と言われており、以前の学年で習った内容をもとに、発展した学習を積み上げていきます。どこを理解していないかはお子さんによって様々です。それを見つけ課題に応じてステップを追って確実に復習することが大切です。ただどこをどの順で復習すればよいのかの判断が難しいこともあります。もし判断に迷ったら、ぜひ、個別指導のプロにご相談ください。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。