中学1年生の数学を乗り切っても、中学2年生でニガテ意識を持つお子さんは少なくありません。ここではニガテ意識を持つお子さんも多い「連立方程式」と、中学2年生数学の最難関といわれる「証明」を中心に、中学2年生の数学の学習のポイントを解説します。
目次
どういう単元で構成されているんだっけ?
 教室長
教室長
中学校の数学って得意でしたか?
 保護者
保護者
得意ではなかったですね。特に計算とか…ほら、式が2つ出てきて、xとyと両方求めるやつとか。
 教室長
教室長
ああ、連立方程式ですね。中学2年生で学習します。
 保護者
保護者
うちの子も連立方程式はニガテみたいです。中学1年生の方程式はそうでもなかったと思うんですけど。
 教室長
教室長
中学1年生の数学ではそれなりにできていたのに、中学2年生になってニガテになるというケースは珍しくありませんよ。
 保護者
保護者
中学2年生の数学って、他にどんなことを勉強していましたっけ。
 教室長
教室長
「連立方程式」に入る前に中学1年生より少し難しくなった「式の計算」、比例を平行移動した「1次関数」、平行線や多角形などの「図形の調べ方」、合同の証明を含む「図形と合同」、そして新しく入ってくる「確率」があります。
 保護者
保護者
そうそう、証明!「2つの三角形が合同であることを証明しなさい」とか「え、これ数学なの?」ってびっくりしましたよね。
 教室長
教室長
中学数学の中ではかなり珍しいタイプの問題ですからね。論理力が試されます。
 保護者
保護者
私もだんだん思い出してきました。連立方程式も証明も、1問を解くのが長くて大変でしたよね。今考えると、中学2年生の数学ってなかなか難しかったんですね。
中2数学の難敵!連立方程式の攻略ポイント
 保護者
保護者
やっぱり、中学2年生の数学の難所は連立方程式だと思うんですよね。
手順が多くて難しいですよね。
 教室長
教室長
連立方程式の難しい点は、大きく3つあります。まず1つ目は、中学1年生までで習う計算ができていなければ解けない、完全な積み上げ単元だということです。
 保護者
保護者
ああ、確かにそうですよね。1次方程式が解けない状態ではどうしようもないです。
 教室長
教室長
おっしゃる通り、1次方程式をなんとなく解いていたお子さんは、連立方程式でつまずくケースが多いです。2つ目は、解き方が一通りではないということです。
 保護者
保護者
少しずつ思い出してきました。2つの式を足したり引いたりするんじゃなくて、まるっと代入する方法がありましたよね。
 教室長
教室長
そうです。前者を「加減法」、後者を「代入法」といいます。基本的にはどちらでも答えを出すことはできるのですが、代入法を学習後にこんがらがって加減法までわからなくなるお子さんが多いですね。パターン暗記をしようとするお子さんに多いケースです。3つ目はその代入法に関することですが、代入の理解不足が挙げられます。1つの文字に多項式を代入できるというのが、うまくイメージできないのですよ。
 保護者
保護者
代入って、たとえば3xにx=2y+5を代入すると、3(2y+5)=6y+15になる、みたいなことでしょうか。
 教室長
教室長
ええ、そうです。変数xが箱のようなもので、数字や文字が1つだけ入るとは限らないということを理解できていないと、この代入はとても難しいんですよ。
 保護者
保護者
そうそう。代入法って、すごくニガテでした。加減法で出したら「そんなに面倒なことをしなくても」って先生に言われて「いや、むしろそっちのほうがわかりません!」って思った記憶があります。
なにか、連立方程式をマスターするよい勉強法ってありますか?
 教室長
教室長
簡単なものからひとつずつ確認していくのがおすすめです。連立方程式はそれまでの積み重ねなので、どこでつまずいているのかがわかりにくいのですよ。ですから、まずはそのまま2式を加減すれば解ける連立方程式からスタート、それが解けなければ、そもそも1次方程式が解けない可能性が高いですから、そこまで戻ってやり直します。
 保護者
保護者
どこでつまずいているのかがわかるように、簡単な問題から少しずつ難しくしていくんですね。
 教室長
教室長
教科書の例題はそういう構成になっていますから、順番に解き直してみるとよいですよ。ニガテなパターンが見つかったら、そこを集中的に練習すれば、必ず解けるようになります。
 保護者
保護者
なるほど。
 教室長
教室長
代入法が入ってきて急にわからなくなったのなら、加減法と混ざってしまっている可能性も高いので、まずは「加減法」と「代入法」という2つの解き方があることを意識することが大切です。その上で、代入法の例題を解いてみるとスッキリしますね。
中2数学の最難関!図形の証明が登場!
 保護者
保護者
連立方程式は反復練習で何とかなりそうだけれど、やっぱり証明は難しい気がします。
 教室長
教室長
図形の証明は好ききらいが分かれますね。数学がニガテなお子さんの中にも証明は得意なお子さんがいたり、逆に比較的数学が得意なのに証明はニガテというお子さんもいらっしゃいます。
 保護者
保護者
証明って、どうすれば得意にできるんでしょうか?
 教室長
教室長
証明は、パターンではなく構造を見極めることが重要なんですよ。
 保護者
保護者
構造ですか?
 教室長
教室長
ええ、骨組みと言ってもよいかもしれませんが、つまりは「言わなければならない柱」です。三角形の合同証明なら、必ず「3つの柱」があるんですよ。三角形の合同条件を覚えていますか?
 保護者
保護者
ええと…3つの辺の長さが同じなら、同じ三角形になりますよね。
 教室長
教室長
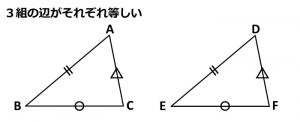
そうですね。「3組の辺がそれぞれ等しい」という合同条件です。
あと「2組の辺とその間の角がそれぞれ等しい」「1組の辺とその両端の角がそれぞれ等しい」の合わせて3つですね。
 保護者
保護者
これが、3つの柱ですか?
 教室長
教室長
いいえ、柱はこの合同条件それぞれに3つずつあるんですよ。たとえば「3組の辺がそれぞれ等しい」は、AB=DE、BC=EF、CA=FDの3つがそろえば使える合同条件なんですよ。
 保護者
保護者
ああ、なるほど。それじゃあ「2組の辺とその間の角がそれぞれ等しい」なら、AB=DE、AC=DF、∠A=∠Dが3つの柱ってことですね。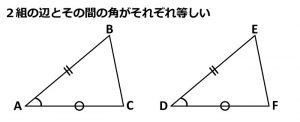
 保護者
保護者
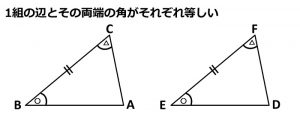
あと1組の辺とその両端の角がそれぞれ等しい」も、BC=EF、∠B=∠E、∠C=∠Fで、やっぱり3つなんですよね。
 教室長
教室長
その通りです。合同の証明は、必要な柱を見つけて、それを説明していくことなんですよ。三角形の合同を証明する場合、最後に必要な条件は必ず3つですから、どの3つを使うのかを決めてから書き始めれば証明もぐっと楽になります。
 保護者
保護者
言われてみると、最初に図の中にいろいろ書き込んで、使う条件を決めてから書き始めていたかもしれませんね。
私は逆に、「△ABC=△DEFにおいて、仮定より…」って書き始めて頭を抱えていた気がします。
 教室長
教室長
証明は、読み手に納得してもらえるように説明することですから、何を言えばよいのかを考えるようにするとぐっとわかりやすくなるんですよ。
 保護者
保護者
だから論理力、なんですね。
難しく考えていたけど、誰かに説明するって考えるとちょっとわかりやすいですねうちの子にも教えてあげなくちゃ。















