今回は、図形やグラフの移動について考えていきましょう。移動とは、図形の形や大きさを変えないで図形の位置だけを変えることです。
中学1年生で、平行移動、回転移動、対称移動を学びます。これらの移動は図形の分野だけでなく、関数のグラフにおいても登場します。その代表的なものが、比例のグラフを平行移動させてできる1次関数のグラフです。
平行移動とはなんだろう?というところからきちんと押さえて、関数のグラフではどのように扱われるかをみていきましょう。わかりやすく解説していきますので、ぜひお子さんのつまずきの解消にお役立てください。平行移動の特徴と作図の方法を確認!
目次
押さえておきたい3つの移動
図形の移動で重要なものは、「平行移動」、「回転移動」、「対称移動」の3つです。これらがどんな移動であったか覚えていらっしゃいますでしょうか? 図とともに確認しておきましょう。
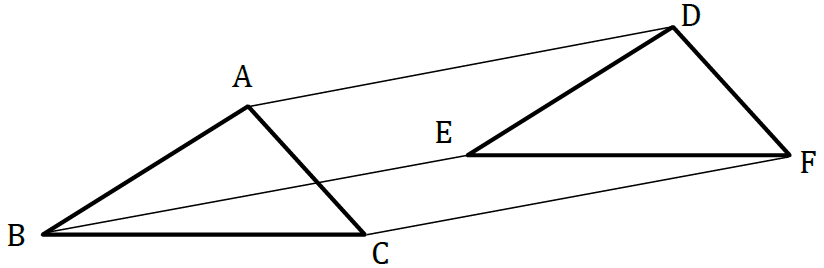
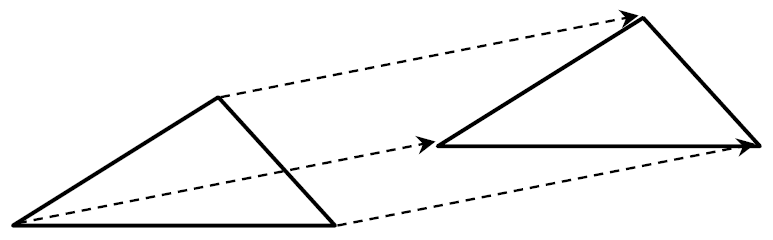
平行移動:平面上で図形を一定の方向に、一定の長さだけずらして、向きを変えずにその図形を移すこと。
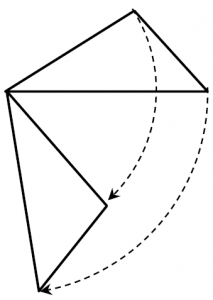
回転移動:平面上で図形を1つの点を中心として、一定の角度だけまわして、向きを変えてその図形を移すこと。
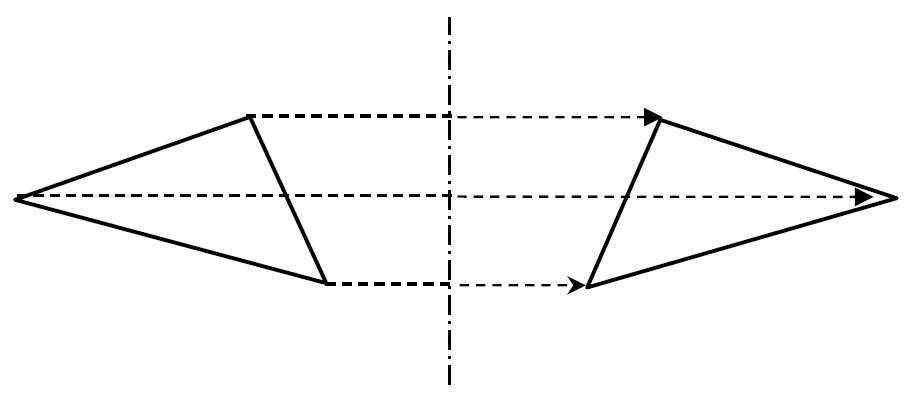
対称移動:図形を1つの直線を折り目として折り返してその図形を移すこと。
これらの図形の移動は、コンパス・定規を使うことで作図ができます。作図の方法はそれぞれの性質や特徴にもとづいていますから、これを知ることで理解が深まります。では、平行移動の作図の方法を見ていきましょう。
三角形の平行移動の作図3つのステップ!
三角形は、3つの頂点で定まります。ですから、3つの頂点を一定の方向に、一定の長さだけずらしてその図形を移せばいいですね。そこで、次の手順で作図します。
① 3つの頂点から、移動させたい方向に直線を引く。
三角定規などを使って、平行な直線を引くことがポイントです。
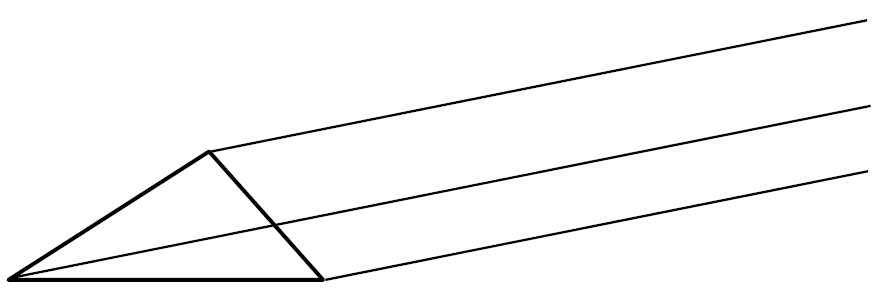
② 移動させたい長さを半径とする円弧を、3つの頂点を中心としてそれぞれかく。
コンパスを使ってかきます。
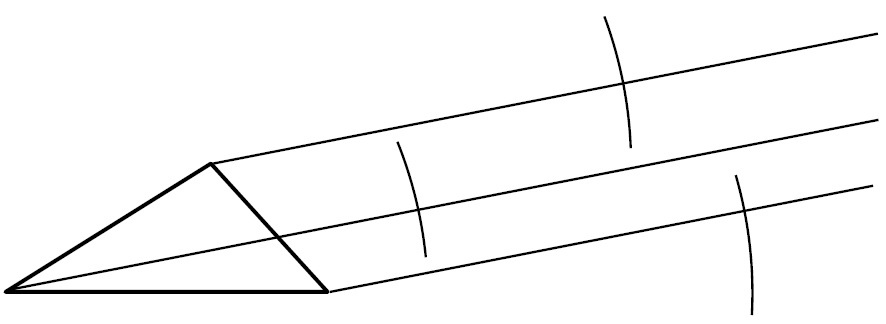
③ ①でかいた直線と②でかいた円弧の交点を結んで三角形をかく。
直線と円弧の組み合わせを間違えないように注意が必要です。
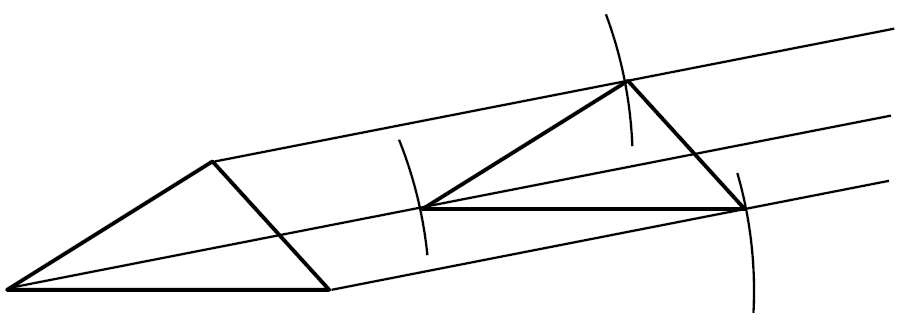
このようにして、平行移動の図形をかくことができます。ここでは三角形を例にとりましたが、何角形でも同じようにかくことができますので、いろいろと試してみてください。
平行移動のポイントは?
平行移動とは、「平面上で図形を一定の方向に、一定の長さだけずらしてその図形を移す」ことですね。つまり、向きと長さ(距離)が定まれば、平行移動を定めたことになることがポイントです。数学では、こういった考え方を身につけることがとても大事です。ぜひお子さんにもお伝えください。では、平行移動についてどのような問題が出されるのかをみていきましょう。
平行移動に関する基本問題を解いてみよう!
移動に関する基本を確認しよう!
|
《例題》
(1) ∠ABC=45°のとき、∠DEFの大きさを答えなさい。 |
ポイントは、「平行移動とは、平面上で図形を一定の方向に、一定の長さだけずらしてその図形を移すこと」です。
(1) は、ずらしただけなので、ずらす前の角の大きさと同じです。よって、
∠DEF=∠ABC=45°
(2) は、平行移動は、同じ方向にずらしているので、平行ですね。
(3) は、平行移動は、同じ長さだけずらしているので、CF=AD=3(cm)
平行移動の基本は確認できたでしょうか? では、関数のグラフの平行移動として代表的な、比例のグラフの平行移動と1次関数のグラフの関係についてみてみましょう。
比例のグラフと1次関数のグラフの関係とは?
比例のグラフをy軸方向に平行移動したら、1次関数のグラフ
比例のグラフを平行移動するとはどういうことでしょうか。例えば、比例y=2xのグラフの平行移動を考えてみましょう。y=2xのグラフは、次のようなグラフです。
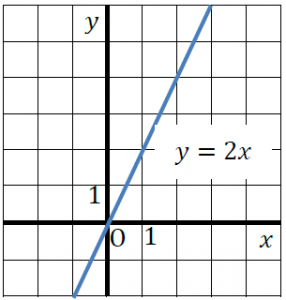
これを、y軸方向に1だけ平行移動してみましょう。すると、
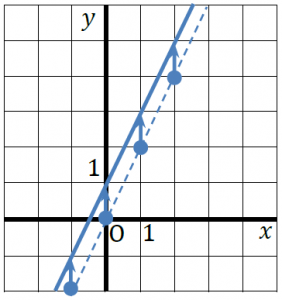
このようなグラフになります。あるxに注目してyの値を考えれば、1だけ大きい値になるので、このグラフの式は、
y=2x+1
ということになります。
1次関数y=ax+bのグラフは、比例y=axのグラフをy軸方向にbだけ平行移動したものであることが、これで確認できます。
比例のグラフを$x$軸方向に平行移動したら?
今度は、x軸方向に1だけ平行移動してみましょう。すると、
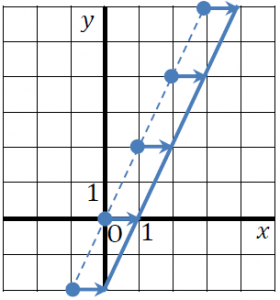

ここまで説明してきた,比例のグラフのx軸方向,y軸方向への移動についてまとめると、
比例y=axのグラフをy軸方向にb、x軸方向にcだけ平行移動したグラフの式は、
y=a(x-c)+b
ということが分かりました。これをグラフで見てみると、次のようになります。
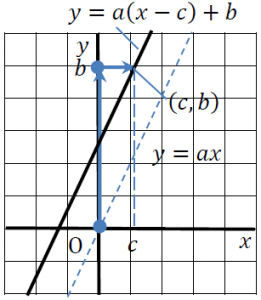
ここから、グラフの傾きがaで、点(c,b)を通る直線の式は、
y=a(x-c)+b
ということも分かります。
では、この直線の式に関する問題をご紹介します。ぜひお子さんと一緒に取り組んでみてください。
東京個別・関西個別(個別指導塾)の基本問題に挑戦!
問題では、比例の式をどのように平行移動するかや、傾きと点の座標が与えられてその式を求めるものが出されます。その際に先ほど紹介した式「y=a(x-c)+b」を使って求めることができます。

今回は、図形の平行移動と、比例のグラフの平行移動から得られる1次関数のグラフについて解説しました。図形や関数はわからないというお子さんもいらっしゃるかと思います。例えばお子さんが1次関数のグラフのかきかたがわからないという場合はどうしますか?かきかたを教えて、漢字の練習のように同じグラフを何回もかかせればかけるようになるのでしょうか?
そもそも1次関数とは何かがわかっていなかったり、傾きの求め方がわかっていなかったり、実は分数がわかっていなかったりということもあるのです。
1人ひとりつまずきポイントは違います。問題をすらすら解けるようになるには、お子さんがどこまで理解しているのかをスモールステップで分析し、つまずきポイントをつきとめて、正しく対処することが重要です。お子さんのつまずきポイントを早く解消したい場合は、個別指導のプロに相談してみるとよいでしょう。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。